You are here: tecnoteca.it » Museo on line » 20. Elaborazione Matematica non Numerica

20. Elaborazione Matematica non Numerica

L'introduzione dei calcolatori programmabili ha rivoluzionato in modo impressionante le capacità di queste macchine ampliando sempre di più le possibili applicazioni. Nel campo matematico si è assistito all'introduzione di sistemi che inglobano sempre di più le facoltà un tempo dominio esclusivo dell'intelligenza umana. Inizialmente, l’ambito di applicazione dei calcolatori programmabili era esclusivamente di tipo numerico: risoluzione di equazioni complesse, interpolazione dati, sistemi lineari e così via. Negli anni ‘50 si prese coscienza del fatto che i calcolatori non sono solo macchine per l’elaborazione di numeri (number crunchers) ma sono strumenti più generali in grado di elaborare informazioni matematiche più complesse. Questa strada, in particolare, è stata aperta con l’elaborazione simbolica.

Fig. 161. Il metodo di Newton-Raphson permette di risolvere equazioni di svariato genere per le quali può anche non esistere alcuna formula risolutiva diretta. Per molto tempo però la notevole mole di calcoli spesso necessari nei vari metodi ha limitato in modo considerevole la loro applicazione. Il calcolatore programmabile ha invece permesso di applicare con grande facilità i diversi metodi numerici grazie all’enorme velocità con cui possono essere svolte le operazioni aritmetiche. Fra l’altro, i moderni calcolatori possono lavorare con un numero di cifre elevato in modo da raggiungere una grande precisione nella risoluzione dei problemi.

Metodo di Newton-Raphson

Il metodo di Newton si utilizza per risolvere un'equazione f(x) = 0, quando f(x) è derivabile in un opportuno intervallo. Partendo da una stima iniziale x₀ della soluzione, si genera una successione {x_k}, dove x_k, sotto opportune ipotesi, rappresenta un'approssimazione sempre migliore della soluzione dell'equazione.

----------------------------------------------------------
Algoritmo. {x stima iniziale della soluzione}
k := 0;
stop := false;
repeat
    y := f(x);
    if abs(y) <= e
        then stop := true
        else x := x - y/df(x);
    if k < nmax
        then k := k + 1
        else stop := true
until stop
----------------------------------------------------------
dove
f(x) = 0  equazione da risolvere
df(x)      funzione derivata di f(x)
nmax    numero massimo di iterazioni

Fig. 162. Un frammento di programma Lisp per il calcolo della derivata simbolica di una funzione. Il Lisp (LISt Processing) è un linguaggio ideato per la ricerca nel campo dell'Intelligenza Artificiale. Progettato da J. Mc Carthy fra il 1957 e il 1960, il Lisp è stato tra i primi dei cosiddetti "linguaggi simbolici", adatto cioè a trattare liste di simboli piuttosto che numeri. Queste capacità hanno permesso di realizzare in seguito programmi sofisticati per l'elaborazione simbolica di operazioni matematiche.

(setf *simplification-rules* (append *simplification-rules* (mapcar #'simp-rule '( (d x / d x = 1) (d (u + v) / d x = (d u / d x) + (d v / d x)) (d (u – v) / d x = (d u / d x) - (d v / d x)) (d (u * v) / d x = u * (d v / d x) + v * (d u / d x)) (d (u / v) / d x = (u * (d v / d x) - v * (d u / d x)) / v ^ 2) (d (u ^ n) / d x = n * u ^ (n – 1) * (d u / d x))

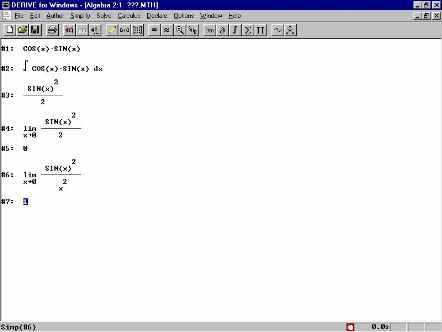
Fig. 163. Calcolo simbolico con il programma Derive. L'introduzione del linguaggio di programmazione Lisp alla fine degli anni '50 (e di altri linguaggi simbolici meno noti) rappresentò una tappa fondamentale per passare nell'ambito dei calcolatori dalla matematica dei numeri alla matematica simbolica delle formule. La notevole flessibilità di questo linguaggio nel trattamento di liste di simboli portò infatti alla sperimentazione e realizzazione di diversi programmi in grado di lavorare su formule simboliche (come ad esempio il calcolo letterale) e non più esclusivamente sui numeri. Uno dei primi programmi in grado di lavorare su espressioni simboliche è stato il sistema SAINT, sviluppato nel 1963 da J. Slage e in grado di lavorare nell'ambito degli integrali indefiniti.

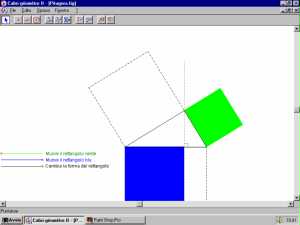
Fig. 164. La geometria con CABRI-GEOMETRE. Questo programma è un ambiente di lavoro per lo studio della geometria piana. In particolare, CABRI permette di focalizzare l'attenzione sulle costruzioni geometriche e, a tale scopo, consente di modificare interattivamente le figure deformandone la forma secondo alcune trasformazioni geometriche.

Fig. 165. Assiomi per la dimostrazione automatica mediante il calcolatore di un teorema nell'ambito della teoria dei gruppi. L'applicazione del calcolatore nel campo della logica matematica portò ad un ulteriore svolta nell'impiego del calcolatore per simulare i "ragionamenti matematici". I primi tentativi in questo senso furono realizzati da Herbert Simon e Allen Newell nel 1955. Nel 1965, l'introduzione di un nuovo e più efficiente metodo logico di dimostrazione (la regola di risoluzione), facilmente automatizzabile, contribuì a stimolare ancora di più la ricerca in questa direzione.

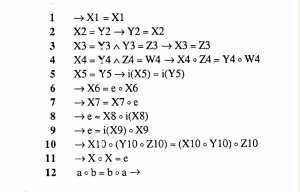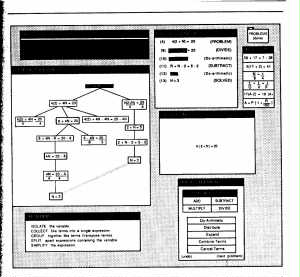
Fig. 166. Una videata del programma Algebrand per l'insegnamento dell'algebra. A partire dagli anni '60 i calcolatori sono stati sperimentati anche nel settore didattico per l'insegnamento della matematica (e di altre discipline) con la realizzazione dei primi programmi CAI (Computer Aided Instruction). Negli anni '70 sono apparsi programmi basati su tecniche di Intelligenza Artificiale con la realizzazione dei cosiddetti Intelligent Tutoring Systems. Questi sistemi, diversamente dai sistemi CAI, non seguono una presentazione degli argomenti rigida e predeterminata ma possono adattare dinamicamente l'interazione con lo studente in base alle specifiche caratteristiche dello studente stesso.

Segnala questa pagina a qualcuno

Stampa questa pagina