Polar Loop
Come la tecnica cartesian loop, anche la tecnica polar loop è di tipo feedback, ossia la linearizzazione è ottenuta forzando l’uscita a seguire l’ingresso. In questo caso, si agisce sulla fase e sull’ampiezza piuttosto che sulle componenti I –Q.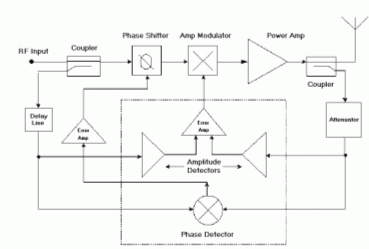
Fig. 10.2: Polar loop: schema a blocchi.
L’architettura polar loop agisce separatamente sulla distorsione di ampiezza e di fase attraverso due anelli di retroazione. L’implementazione che si intende analizzare è innovativa, nel senso che il confronto della fase e dell’ampiezza non avviene in banda base o ad una frequenza intermedia, come si faceva originariamente per semplificare il processo di rilevazione, reso oggigiorno più semplice dai recenti progressi dei circuiti integrati analogici.
In fig. 10.2 è mostrato un diagramma a blocchi semplificato del polar loop: gli errori di fase e ampiezza sono rilevati dal confronto tra i segnali di riferimento e di uscita. L’errore di ampiezza deriva dalla differenza tra gli inviluppi dei segnali di riferimento e di feedback; analogamente per l’errore di fase. Questi errori sono amplificati ( o integrati ) e usati per pilotare modulatori nel ramo diretto.
Un problema rilevante è il tempo di ritardo nel sistema. In effetti, si confronta il riferimento privo di ritardo con il segnale di feedback, ritardato dal percorso del ramo diretto, dall’amplificatore e dal ramo di feedback. E’ possibile ovviare a ciò usando una linea di ritardo lungo il percorso del segnale di riferimento, cosicché il confronto avviene nello stesso istante. Ciò limita la larghezza di banda dell’errore; la linea di ritardo può essere omessa per applicazioni a banda stretta quando la variazione di fase è molto piccola e può essere contenuta dall’anello.
In genere, la larghezza di banda della modulazione è molto più piccola della portante RF al punto che le variazioni di fase e dell’inviluppo oltre i tempi di ritardo dei circuiti sono minimizzabili.
Come regola generale, la larghezza di banda dell’errore necessita essere cinque volte la larghezza di banda del segnale modulante.
Un’analisi matematica sul controllo dell’ampiezza, può far meglio comprendere il funzionamento del polar loop; analoga analisi può essere fatta sul controllo della fase.
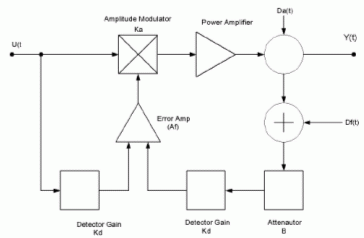
Fig 11.2: Polar loop: diagramma di flusso.
Con riferimento alla fig. 11.2, siano:
- Da(t) la distorsione generata nel PA;
- Df(t) è la distorsione prodotta dal ramo di retroazione;
- A è il guadagno del PA;
- B è il fattore di attenuazione;
- Ka è il modulatore d’ampiezza;
- Af è il guadagno dell’amplificatore nel ramo di retroazione;
- Kd è il guadagno dello stadio rilevatore d’ampiezza;
- U(t) è il segnale di ingresso;
- Y(t) è il segnale di uscita;
procedendo nell’analisi:
Y(t) = A ( U(t) + F(t) ) + Da(t)
dove F(t) è l’errore d’ampiezza:
F(t) = Kd Af Ka ( U(t) – B Y(t) + B Df(t) ),
quindi, posto K = Kd Af Ka risulta:
Y(t) = U(t) + K ( U(t) – B Y(t) + B Df(t) ) + Da(t).
Nell’ipotesi che A B K >> 1 e K >>1, risolvendo si ha:
![]()
B setta il guadagno d’anello chiuso; ogni distorsione causata dal PA è ridotta dal guadagno d’anello ABK.
Ad un guadagno d’anello di 20 dB corrisponderebbe una riduzione di 20 dB su ogni prodotto di intermodulazione che cade nella banda in cui opera l’anello (13).
Confrontando queste due architetture di tipo feedback, uno dei benefici del cartesian loop rispetto al polar loop è la simmetria del guadagno e la banda dei due segnali in quadratura. Ciò riduce la tendenza a introdurre lo spostamento di fase attraverso i meccanismi non lineari di conversione AM/AM e AM/PM che affliggono tutti i sistemi di correzione. Tuttavia la banda e la stabilità limitano la capacità di operare su più portanti. Inoltre data la vasta disponibilità a basso costo di modulatori e demodulatori I – Q, complessivamente il sistema sembra essere un’architettura semplice e interessante per realizzare la linearizzazione in un trasmettitore (8).

